The speed-time graph of a particle moving along a fixed direction is shown in figure below:
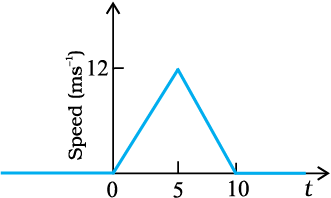
What is the average speed of the particle over the interval \(t=0~\text s\) to \(t=10~\text s?\)
1. \(3~\text{m/s}\)
2. \(6~\text{m/s}\)
3. \(12~\text{m/s}\)
4. \(0~\text{m/s}\)
(a) Distance travelled by the particle = Area under the given graph
= (1/2) × (10 - 0) × (12 - 0) = 60 m
Average speed = Distance / Time = 60 / 10 = 6 m/s
(b)Let s1 and s2 be the distances covered by the particle between time
t = 2 s to 5 s and t = 5 s to 6 s respectively.
Total distance (s) covered by the particle in time t = 2 s to 6 s
s = s1 + s2
For distance s1
Let u1 be the velocity of the particle after 2 s and a1 be the acceleration of the particle in t = 0 to t = 5 s.
Since the particle undergoes uniform acceleration in the interval t = 0 to t = 5 s, from the first equation of motion, acceleration can be obtained as:
v = u + at
Where,
v = Final velocity of the particle
12 = 0 +a1 × 5
Again, from the first equation of motion, we have velocity at t=2sec
v = u + at
u1= 0 + 2.4 × 2 = 4.8 m/s
Distance travelled by the particle between time 2 s and 5 s i.e., in 3 s
= 25.2 m ........(i)
For distance s2:
Let a2 be the acceleration of the particle between time t = 5 s and t = 10 s.
From first equation of motion,
v = u + at (where v = 0 as the particle finally comes to rest)
0 = 12 + a2 × 5
a2 = -12 / 5 = - 2.4 m/s2
Distance travelled by the particle in 1s (i.e., between t = 5 s and t = 6 s)
= 12 - 1.2 = 10.8 m .........(ii)
From equations (i) and (ii) we get
s = 25.2 + 10.8 = 36 m
Therefore,
Average speed = Total distance/time taken = 36 / 4 = 9 m/s.

© 2026 GoodEd Technologies Pvt. Ltd.