The pressure-volume work for an ideal gas can be calculated by using the expression .
The work can also be calculated from the pV-plot by using the area under the curve within the specified limits.
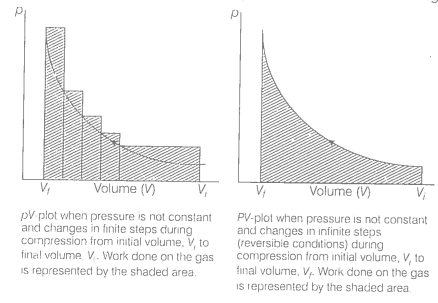
An ideal gas is compressed (a) reversibly or (b) irreversibly from volume to .
The correct option is:
1.
2.
3.
4.
In a reversible process, the reaction occurs very slowly, with the external driving force only infinitesimally greater than the opposing force within the system. This gradual change allows the system to pass through a series of equilibrium states, resulting in minimal energy dissipation during work done by the system.
In contrast, an irreversible process is rapid, shifting the system directly from the initial to the final state without intermediate equilibrium stages. As a result, energy dissipation is higher due to the sudden change.
Consider isothermal compression of a gas from volume ( \(V_1\)) to (\( V_2 \)), where the external pressure (\( P_{\text{ext}} \)) is slightly higher than the gas pressure(P). During compression, system pressure increases as volume decreases, but for a reversible process, this change happens gradually, as shown in the P-V curve.

In a reversible process, the energy dissipated is minimal, resulting in a deep, smooth P-V curve due to the gradual transition through equilibrium states.
In an irreversible process, however, the system undergoes a sudden shift from \(P_1V_1\) to \(P_2V_2\), creating a straight line on the P-V diagram that directly connects the initial and final states without intermediate points.

Calculating the area under the curve reveals that the area for a reversible compression is smaller than the area under the curve for an irreversible isothermal compression of the gas.
Thus, we have \(\text { w(reversible) < w(irreversible) }\)
A reaction at equilibrium is reversible. Conversely, a reaction that is not at equilibrium is irreversible. All real processes are irreversible.
Reversible processes produce the maximum amount of work
If a process does work on the surroundings, you get more work out of the process if it is done slowly. This is because less heat is lost to the surroundings. So a reversible process (infinitely slow) does the maximum work. There is one example of this that is easy to understand: the work done by a gas expanding inside a piston. We will see that the maximum amount of work is obtained when the gas is allowed to expand very slowly (reversibly).