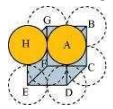
(i) Simple cubic
In a simple cubic lattice, the particles are located only at the corners of the cube and touch each other along the edge.
Let the edge length of the cube be ‘a’ and the radius of each particle be r.
So, we can write:
a = 2r
Now, volume of the cubic unit cell = a3
= (2r)3
= 8r3
We know that the number of particles per unit cell is 1.
Therefore, volume of the occupied unit cell
Hence, packing efficiency
(ii) Body-centred cubic
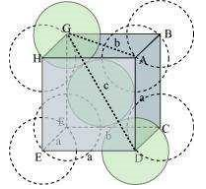
It can be observed from the above figure that the atom at the centre is in contact with the other two atoms diagonally arranged.
From ∆FED, we have:
Again, from ∆AFD, we have:
Let the radius of the atom be r.
Length of the body diagonal, c = 4
Volume of the cube,
A body-centred cubic lattice contains 2 atoms.
So, volume of the occupied cubic lattice
(iii) Face-centred cubic
Let the edge length of the unit cell be ‘a’ and the length of the face diagonal AC be b.
From ∆ABC, we have:
Let r be the radius of the atom.
Now, from the figure, it can be observed that:
Now, volume of the cube,
We know that the number of atoms per unit cell is 4.
So, volume of the occupied unit cell