Match the type of unit cell given in Column I with the features given in Column II.
| Column I | Column II | |||
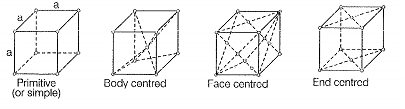
| A | Primitive cubic unit cell | 1. | Each of the three perpendicular edges compulsorily have the different edge length i.e., a ≠ b ≠ c | |
| B | Body centred cubic unit cell | 2. | Number of atoms per unit cell is one. | |
| C | Face centred cubic unit cell | 3. | Each of the three perpendicular edges compulsorily have the same edge length i.e., a=b=c | |
| D | End centred orthorhombic | 4. | In addition to the contribution from the corner unit cell atoms the number of atoms present in a unit cell is one | |
| 5. | In addition to the contribution from the corner atoms the number of atoms present in a unit cell is three | |||
Codes:
| Options: | A | B | C | D |
| 1. | 2,5 | 3,1 | 4,2 | 1,3 |
| 2. | 1 | 2 | 3 | 5 |
| 3. | 2,3 | 3,4 | 3,5 | 1,4 |
| 4. | 4 | 5 | 3 | 2 |
Total number of atoms per unil cell = 1/8x 8=1
Here, 1/8 is due to contribution of each atom present at corner.
B. For body centred cubic unit cell, a=b=c
This lattice contain atoms at corner as well as body centre. Contribution duo to atoms at corner = 1/8 x 8 = 1contribution due to atoms at body centre = 8
C. For face centred unit cell, a=b=c
Total constituent Ions per unit cell present at corners = x 8 = 1
Total constituent ions per unit cell present at face centre = x 6 = 3
D. For end centered orthorhombic unit cell, abc
Total contribution of atoms present at corner
Total contribution of atoms present at end centre
Hence, other than corner it contain total one atom per unit cell.

© 2026 GoodEd Technologies Pvt. Ltd.