Ncert Exercises & Solutions

4.22 $\vec{ı} and \vec{ȷ}$ are unit vectors along x- and y- axis respectively. What is the magnitude and direction of the vectors

$\vec{ı} + \vec{j}$ , and $\vec{ı} - \vec{j}$ ? What are the components of a vector

$\vec{A} = \vec{2 ı} and 3 \overset{⇀}{j}$

along the directions of $\vec{ı} + \vec{ȷ}$ and

$\vec{ı} - \vec{ȷ}$ ? [You may use graphical method]

NEETprep Answer:

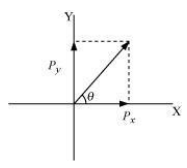
Consider a vector 𝑃⃗⃗, given as:

$\bar{P} = \hat{i} + \hat{j}$

$P_{x} \hat{i} + P_{y} \hat{j} = \hat{i} + \hat{j}$

On comparing the components on both sides, we get:

$\begin{array}{l} P_{x} = P_{y} = 1 \\ \vec{1 P 1} = \sqrt{P_{x}^{2} + P_{y}^{2}} = \sqrt{1^{2} + 1^{2}} = \sqrt{2} \end{array}$

Hence, the magnitude of the vector

$\vec{ı} + \vec{ȷ}$ is

$\sqrt{2}$ .

Let 𝜃 be the angle made by the vector 𝑃⃗⃗, with the x-axis, as shown in the following figure.

$\begin{array}{l} ∴ \tan θ = (\frac{P_{y}}{P_{x}}) \\ θ = \tan^{- 1} (\frac{1}{1}) = 45^{\circ} \end{array}$

Hence, the vector

$\hat{i} + \hat{j}$ makes an angle of 45° with the x-axis.

$\begin{array}{l} Let \vec{Q} = \hat{i} - \hat{j} \\ Q_{x} \hat{i} - Q_{y} \hat{j} = \hat{i} - \hat{j} \\ Q_{x} = Q_{y} = 1 \\ | \bar{Q} | = \sqrt{Q_{x}^{2} + Q_{y}^{2}} = \sqrt{2} \end{array}$

Hence, the magnitude of the vector

$\vec{ı} - \vec{ȷ}$ is √2.

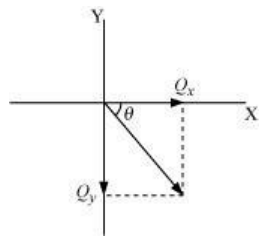
Let 𝜃 be the angle made by the vector

$\vec{Q}$ , with the x-axis, as shown in the following figure.

$\begin{array}{l} ∴ \tan θ = (\frac{Q_{y}}{Q_{x}}) \\ θ = - \tan^{- 1} (- \frac{1}{1}) = - 45^{\circ} \end{array}$ Hence, the vector

$\vec{ı} - \vec{ȷ}$ makes an angle of -45° with the x-axis.

It is given that:

$\begin{array}{l} \vec{A} = 2 \hat{i} + 3 \hat{j} \\ A_{x} \hat{i} + A_{y} \hat{j} = 2 \hat{i} + 3 \hat{j} \end{array}$ On comparing the coefficients of

$\vec{i}$ and

$\vec{j}$ , we have:

$\begin{array}{l} A_{x} = 2 and A_{y} = 3 \\ | \vec{A} | = \sqrt{2^{2} + 3^{2}} = \sqrt{13} \end{array}$ Let

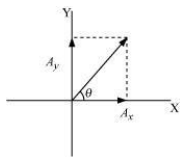
$\vec{A_{x}}$ make an angle 𝜃 with the x-axis, as shown in the following figure.

$\begin{array}{l} ∴ \tan θ = (\frac{A_{y}}{A_{x}}) \\ θ = \tan^{- 1} (\frac{3}{2}) \\ = \tan^{- 1} (1.5) = {56.31}^{\circ} \end{array}$

The angle between the vectors

$(2 \hat{i} + 3 \hat{j}) and (\hat{i} + \hat{j}), θ = 56.31 - 45 = {11.31}^{\circ}$

Component of vector

$\vec{A}$ , along the direction of

$\vec{P}$ , making and angle 𝜃.

$\begin{array}{l} = (A \cos θ) \hat{P} = (A \cos 11.31) \frac{(\hat{i} + \hat{j})}{\sqrt{2}} \\ = \sqrt{13} \times \frac{0.9806}{\sqrt{2}} (\hat{i} + \hat{j}) \\ = 2.5 (\hat{i} + \hat{j}) \\ = \frac{25}{10} \times \sqrt{2} \\ = \frac{5}{\sqrt{2}} \end{array}$ Let

$θ$ be the angle between the vectors

$(2 \hat{i} + 3 \hat{j}) and (\hat{i} - \hat{j})$

$θ^{''} = 45 + 56.31 = {101.31}^{\circ}$

Component of vector 𝐴⃗, along the direction of 𝑄⃗⃗, making and angle 𝜃.

$\begin{array}{l} = (A \cos θ^{''}) \bar{Q} = (A \cos θ) \frac{i - j}{\sqrt{2}} \\ = \sqrt{13} \cos ({901.31}^{\circ}) \frac{(\hat{i} - \hat{j})}{\sqrt{2}} \\ = - \sqrt{\frac{13}{2}} \sin {11.30}^{\circ} (\hat{i} - \hat{j}) \\ = - 2.550 \times 0.1961 (\hat{i} - \hat{j}) \\ = - 0.5 (\hat{i} - \hat{j}) \\ = - \frac{5}{10} \times \sqrt{2} \\ = - \frac{1}{\sqrt{2}} \end{array}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions