20 October - Work, Energy and Power Contact Number: 9667591930 / 852752171820 October - Work, Energy and Power Contact Number: 9667591930 / 8527521718A spring 40 mm long is stretched by the application of a force. If 10 N force required to stretch the spring through 1 mm, then work done in stretching the spring through 40 mm is
1. 84J
2. 68J
3. 23J
4. 8J
A particle is moving on the circular path of the radius (R) with centripetal acceleration . Then the correct relation showing power (P) delivered by net force versus time (t) is 
1. 1
2. 2
3. 3
4. 4
A body is displaced from (0,0) to (1m,1m) along the path x=y by a force . The work done by this force will be :
1.
2.
3.
4.
A weightless rod of length 2l carries two equal mass 'm', one tied at lower end A and the other at the middle of the rod at B. The rod can rotate in a vertical plane about a fixed horizontal axis passing through C. The rod is released from rest in the horizontal position. The speed of the mass B at the instant rod becomes vertical is:
1. \(\sqrt{\frac{3 g l}{5}} \)
2. \(\sqrt{\frac{4 g l}{5}} \)
3. \(\sqrt{\frac{6 g l}{5}} \)
4. \(\sqrt{\frac{7 g l}{5}} \)
As per the given figure to complete the circular loop, what should be the radius of the loop?
1. 4 m
2. 3 m
3. 2.5 m
4. 2 m
A force acts on a 30 gm particle in such a way that the position of the particle as a function of time is given by , where x is in metres and t is in seconds. The work done during the first 4 seconds is
(1) 5.28 J
(2) 450 mJ
(3) 490 mJ
(4) 530 mJ
A particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement x is proportional to-
(1) x2
(2) ex
(3) x
(4) loge x
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k. The maximum compression in the spring is x then-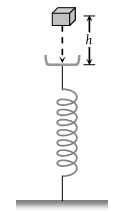
(1)
(2)
(3)
(4)
An open knife edge of mass 'm' is dropped from a height 'h' on a wooden floor. If the blade penetrates upto the depth 'd' into the wood, the average resistance offered by the wood to the knife edge is
(1) mg
(2)
(3)
(4)
The force acting on a body moving along x-axis varies with the position of the particle as shown in the fig.
The body is in stable equilibrium at
(1) x = x1
(2) x = x2
(3) both x1 and x2
(4) neither x1 nor x2
A ball is thrown vertically downwards from a height of \(20\) m with an initial velocity \(v_0\). It collides with the ground, loses \(50\%\) of its energy in a collision and rebounds to the same height. The initial velocity \(v_0\) is: (Take \(g = 10~\text{m/s}^2\))
1. \(14~\text{m/s}\)
2. \(20~\text{m/s}\)
3. \(28~\text{m/s}\)
4. \(10~\text{m/s}\)
The potential energy of a system increases if work is done
(1) by the system against a conservative force
(2) by the system against a nonconservative force
(3) upon the system by a conservative force
(4) upon the system by a nonconservative force
The points of maximum and minimum attraction in the curve between potential energy (U) and distance (r) of a diatomic molecules are respectively -
(1) S and R
(2) T and S
(3) R and S
(4) S and T
Two balls having different masses are moving towards each other with speed 30 m/s and 20 m/s as shown in figure (i). Their velocities after collision become 20 m/s and 30 m/s as shown in the figure (ii), then the coefficient of restitution is: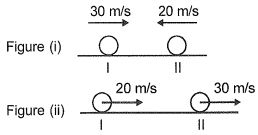
(1) 1
(2) 0.5
(3) 0.4
(4) 0.2
A smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision, their final velocities are V and v respectively. The value of v is:-
1.
2.
3.
4.
