A straight section PQ of a circuit lies along the X-axis from x= to x= and carries a steady current i. The magnetic field due to the section PQ at a point X = + a will be:
1. Proportional to a 2. Proportional to
3. Proportional to 4. Zero
A circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r >> R, varies as
1.
2.
3.
4.
In the figure shown, the magnetic induction at the centre of the arc due to the current in portion AB will be
1. 3.
2. 4. Zero
In the figure shown below there are two semicircles of radius \(r_1\) and \(r_2\) in which a current \(i\) is flowing. The magnetic induction at the centre of \(O\) will be:
| 1. | \(\dfrac{\mu_{0} i}{r} \left(r_{1} + r_{2}\right)\) | 2. | \(\dfrac{\mu_{0} i}{4} \left[\dfrac{r_{1} + r_{2}}{r_{1} r_{2}}\right]\) |
| 3. | \(\dfrac{\mu_{0} i}{4} \left(r_{1} - r_{2}\right)\) | 4. | \(\dfrac{\mu_{0} i}{4} \left[\dfrac{r_{2} - r_{1}}{r_{1} r_{2}}\right]\) |
The magnetic field at the centre of a coil of n turns, bent in the form of a square of side 2 l, carrying current i, is :
1. 2.
3. 4.
A and B are two concentric circular conductors of centre O and carrying currents and as shown in the adjacent figure. If ratio of their radii is 1 : 2 and ratio of the flux densities at O due to A and B is 1 : 3, then the value of is
1. 2.
3. 4.
A small coil of N turns has an effective area A and carries a current I. It is suspended in a horizontal magnetic field such that its plane is perpendicular to . The work done in rotating it by about the vertical axis is
1. 2.
3. 4.
The magnetic field at the centre of a circular coil of radius r is times that due to a long straight wire at a distance r from it, for equal currents. Figure here shows three cases : in all cases the circular part has radius r and straight ones are infinitely long. For same current the B field at the centre P in cases 1, 2, 3 have the ratio
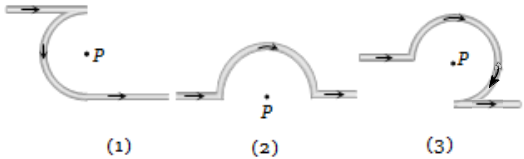
1.
2.
3.
4.
A cell is connected between the points A and C of a circular conductor ABCD of centre O with angle AOC = . If and are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio is:
1. 0.2
2. 6
3. 1
4. 5
A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic field vector at a point having coordinates (x, y) in the z = 0 plane is :
1.
2.
3.
4.
| 1. |  |
2. |  |
| 3. |  |
4. |  |
A particle with charge \(q\), moving with a momentum \(p\), enters a uniform magnetic field normally. The magnetic field has magnitude \(B\) and is confined to a region of width \(d\), where \(d< \frac{p}{Bq}.\) The particle is deflected by an angle \(\theta\) in crossing the field, then:

| 1. | \(\sin \theta=\frac{Bqd}{p}\) | 2. | \(\sin \theta=\frac{p}{Bqd}\) |
| 3. | \(\sin \theta=\frac{Bp}{qd}\) | 4. | \(\sin \theta=\frac{pd}{Bq}\) |
A current-carrying loop is placed in a uniform magnetic field in four different orientations, I, II, III & IV. The decreasing order of potential energy is:

| 1. | I > III > II > IV | 2. | I > II >III > IV |
| 3. | I > IV > II > III | 4. | III > IV > I > II |
The relation between voltage sensitivity () and current sensitivity () of a moving coil galvanometer is (Resistance of Galvanometer = G)
1.
2.
3.
4.
| 1. | \(\frac{1}{2}\) | 2. | \(1\) |
| 3. | \(4\) | 4. | \(\frac{1}{4}\) |