The equivalent capacitance between A and B is as the given figure:

 
1. $16 \pi \epsilon_ 0 r$
2. $4 \pi \epsilon_ 0 r$
3. $8 \pi \epsilon_ 0 r$
4. None of these

Two metallic spheres of radii 2cm and 3cm are given charges 6mC and 4mC respectively. The final charge on the smaller sphere will be if they are connected by a conducting wire

1. 4mC

2.6mC

3. 5mC

4. 10mC

In the circuit shown in the figure, the energy stored in $6~\mu\text{F}$ capacitor will be:
      

The figure shows some of the equipotential surfaces. Magnitude and direction of the electric field is given by

1. 200 V/m, making an angle ${120}^0$ with the x-axis

2. 100 V/m, pointing towards the negative x-axis

3. 200 V/m, making an angle $-{60}^0$ with the x-axis

4. 100 V/m, making an angle ${30}^0$ with the x-axis

An air capacitor of capacity $C=10\mu F$ is connected to a constant voltage battery of 12 V. Now the space between the plates is filled with a liquid of dielectric constant 5. The charge that flows now from battery to the capacitor is

1. 120 $\mu C$

2. 699 $\mu C$

3. 480 $\mu C$

4. 24 $\mu C$

A and B are two concentric metallic shells. If A is positively charged and B is earthed, then electric

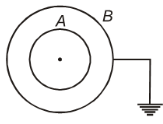
1.  Field at common centre is non-zero

2.  Field outside B is nonzero

3.  Potential outside B is positive

4.  Potential at common centre is positive

$\mathrm{The} \mathrm{electric} \mathrm{potential} \mathrm{at} \mathrm{a} \mathrm{point} \mathrm{at} \mathrm{distance} \sqrt{3}\mathrm{R} \mathrm{from} \mathrm{the} \mathrm{centre} \mathrm{of} \mathrm{disc}$
$\mathrm{of} \mathrm{radius} \mathrm{R} \mathrm{lying} \mathrm{in} \mathrm{the} \mathrm{axis} \mathrm{of} \mathrm{the} \mathrm{disc} \mathrm{whose} \mathrm{surface} \mathrm{charge} \mathrm{density} \mathrm{is} \mathrm{\sigma }$
$\mathrm{will} \mathrm{be} \mathrm{given} \mathrm{by}:$
$1. \frac{\sigma }{2{\epsilon }_0}\left[2-\sqrt{3}\right]R 2. \frac{\sigma }{2{\epsilon }_0}\left[2+\sqrt{3}\right]R$
$3.\frac{\sigma }{2{\epsilon }_0}\left[\sqrt{3}-\sqrt{2}\right]R 4. \frac{\sigma }{2{\epsilon }_0}\left[\sqrt{3}+\sqrt{2}\right]R$

An elementary particle of mass m and charge e is projected with velocity v at a much more massive particle of charge Ze, where Z>0. What is the closest possible approach of the incident particle ?

1. $\frac{Z{e}^2}{2\pi {\epsilon }_{0}m{v}^2}$​

2. $\frac{Ze}{4\pi {\epsilon }_{0}m{v}^2}$

3. $\frac{Z{e}^2}{8\pi {\epsilon }_{0}m{v}^2}$​

4. $\frac{Ze}{8\pi {\epsilon }_{0}m{v}^2}$