A block $P$ of mass $m$ is placed on a frictionless horizontal surface. Another block $Q$ of same mass is kept on $P$ and connected to the wall with the help of a spring of spring constant $k$ as shown in the figure. $\mu_s$ is the coefficient of friction between $P$ and $Q$. The blocks move together performing SHM of amplitude $A$. The maximum value of the friction force between $P$ and $Q$ will be:

         
1. $kA$
2. $\frac{kA}{2}$
3. zero
4. $\mu_s mg$

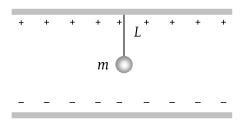
A small sphere carrying a charge ‘q’ is hanging in between two parallel plates by a string of length L. Time period of pendulum is T₀. When parallel plates are charged, the electric field between the plates is E and time period changes to T. The ratio T/T₀ is equal to 

(1) ${\left(\frac{{\displaystyle g+\frac{{\displaystyle qE}}{{\displaystyle m}}}}{{\displaystyle g}}\right)}^{1/2}$           (2) ${\left(\frac{{\displaystyle g}}{{\displaystyle g+\frac{{\displaystyle qE}}{{\displaystyle m}}}}\right)}^{3/2}$

(3) ${\left(\frac{{\displaystyle g}}{{\displaystyle g+\frac{{\displaystyle qE}}{{\displaystyle m}}}}\right)}^{1/2}$           (4) None of these 

A second's pendulum is mounted in a rocket. Its period of oscillation decreases when the rocket:

1. Comes down with uniform acceleration

2. Moves around the earth in a geostationary orbit

3. Moves up with a uniform velocity

4. Moves up with the uniform acceleration

A particle executes linear simple harmonic motion with an amplitude of of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of its velocity  is equal to that of its acceleration. Then, its time period in seconds is 

1. $\sqrt{\frac{5}{\pi }}$

2.$\sqrt{\frac{5}{2\mathrm{\pi }}}$

3. $\frac{4\mathrm{\pi }}{\sqrt{5}}$

4. $\frac{2\mathrm{\pi }}{\sqrt{3}}$

A body mass m is attached to the lower end of a spring whose upper end is fixed. The spring has neglible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1 kg, the time period of oscillations becomes 5s. The value of m in kg is-

1. $\frac{3}{4}$               

2. $\frac{4}{3}$

3. $\frac{16}{9}$               

4. $\frac{9}{16}$

When two displacements represented by y₁=asin(ωt) and y₂=bcos(ωt) are superimposed,the motion is -

1. not a simple harmonic

2. simple harmonic with amplitude a/b

3. simple harmonic with amplitude $\sqrt{a^{2 }+ b^2}$

4. simple harmonic with amplitude (a+b)/2

The damping force on an oscillator is directly proportional to the velocity. The units of the constant of proportionality are 

1.$\mathrm{ k}g m{s}^{-1}$                               

2.$\mathrm{ k}g m{s}^{-2}$

3. $kg s^{-1}$                                   

4. $kg s$